你有没有想过,一张看似完整的方格纸,竟然会在不经意间消失一个正方形?这可不是普通的魔术表演,而是数学世界中的一个奇妙谜题——失踪的正方形。今天,就让我们一起揭开这个谜题的神秘面纱,看看那个消失的正方形究竟去哪儿了!

想象你手中有一张画满了正方形的方格纸。按照图示,你小心翼翼地将它切割成五小块,然后按照另一种方式重新拼接。神奇的事情发生了,原本应该有的正方形竟然不见了!这可不是普通的魔术,而是数学大师马丁·加德纳在1961年提出的“失踪的正方形”谜题。
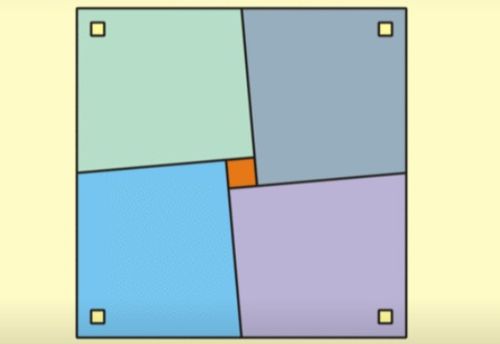
这个谜题的关键在于,我们看到的图形并不是真正的三角形,而是看似三角形但实际上是凹四边形和凸四边形的组合。红色和蓝色三角形的斜边斜率略有差异,这让我们误以为它们是直角三角形。实际上,这两个图形并不是同一个长宽比,因此斜边在拼接过程中实际上缩短了。
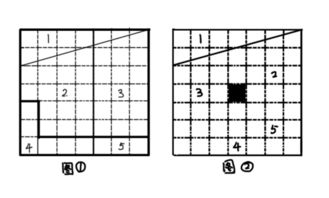
当我们将两张图重叠时,会发现一个细微的平行四边形,它恰好占据了一格的面积。这个平行四边形就是失踪的正方形。这个谜题的关键在于,我们往往无法察觉到这样细微的差别,因此才会觉得正方形消失了。
更令人惊讶的是,失踪的正方形谜题中描述的整数域(2,3,5,8,13)竟然是连续的斐波那契数。斐波那契数列是数学中一个著名的数列,它以0和1开始,后面的每个数都是前两个数的和。这个数列的奇妙之处在于,它几乎无处不在,从自然界到艺术,从科学到金融,斐波那契数列都展现出了它的神奇魅力。
失踪的正方形谜题不仅是一个有趣的数学游戏,它还可以应用于实际生活中。例如,在建筑设计中,我们可以利用这个谜题来避免类似的问题,确保建筑物的几何形状准确无误。
失踪的正方形谜题最初是由纽约市业余魔术师保罗·嘉理在1953年发明的。这个谜题的原理早在1860年就已经为数学家所知。失踪的正方形谜题的发明,不仅展示了数学的奇妙,也体现了人类对未知世界的好奇和探索精神。
失踪的正方形谜题是一个充满趣味和挑战的数学谜题。它不仅让我们领略到了几何图形的奇妙,还揭示了斐波那契数列的神秘。这个谜题告诉我们,数学世界充满了无限的可能,只要我们用心去探索,就能发现其中的奥秘。那么,你准备好揭开失踪的正方形的秘密了吗?